Tensorflow (Probability) で線形回帰

モデル

$D$ 次元データを $N$ 個観測したときに以下のモデルを考える。

y=X\beta+\varepsilon

ただし、 $y=(y_1,\cdots,y_N)^{\top},X=(x_1^{\top},\cdots,x_N^{\top})^{\top},x_i=(1,x_{i1},\cdots,x_{iD})^{\top},\beta=(\beta_0,\cdots,\beta_{D})^{\top},\varepsilon=(\varepsilon_1,\cdots,\varepsilon_N)$ 、すべて実数値である。それぞれ、以下のように真のデータを生成することにする。

x_{ij}\sim{\rm Uniform}(0,1) \\ \beta_j\sim{\rm Uniform}(-1,1) \\ \varepsilon_i\sim{\rm Normal}(0,\sigma^2) \\

データ生成

まずは、 $N,D,\sigma^2$ の値を決める。ノイズの分散 $\sigma^2$ は $x_{ij},\beta_j$ に対して適度に小さな値にしておく。

N = 100   # number of data (= observations)
D = 5   # number of dimensions (= features)
variance = 0.1   # of noise

そして、上のモデルにしたがって観測データをランダムに生成する。データ $X,y$ および真のパラメタ $\beta$ は推定したいわけではないので、np.ndarrayで持つ。tf.constantで持ってもよいが、eager execution でないと実際の値が分からないし、特にメリットは無いように思う。tf.Variableオブジェクトは評価のたびに生成し直されてしまうのでダメ。

dtype = np.float32
beta_true = np.random.uniform(-1, 1, [D + 1, 1]).astype(dtype)
X = np.concatenate([np.ones([N, 1]),
                    np.random.uniform(0, 1, [N, D])], axis=1).astype(dtype)
e = np.random.normal(0, np.sqrt(variance), [N, 1]).astype(dtype)
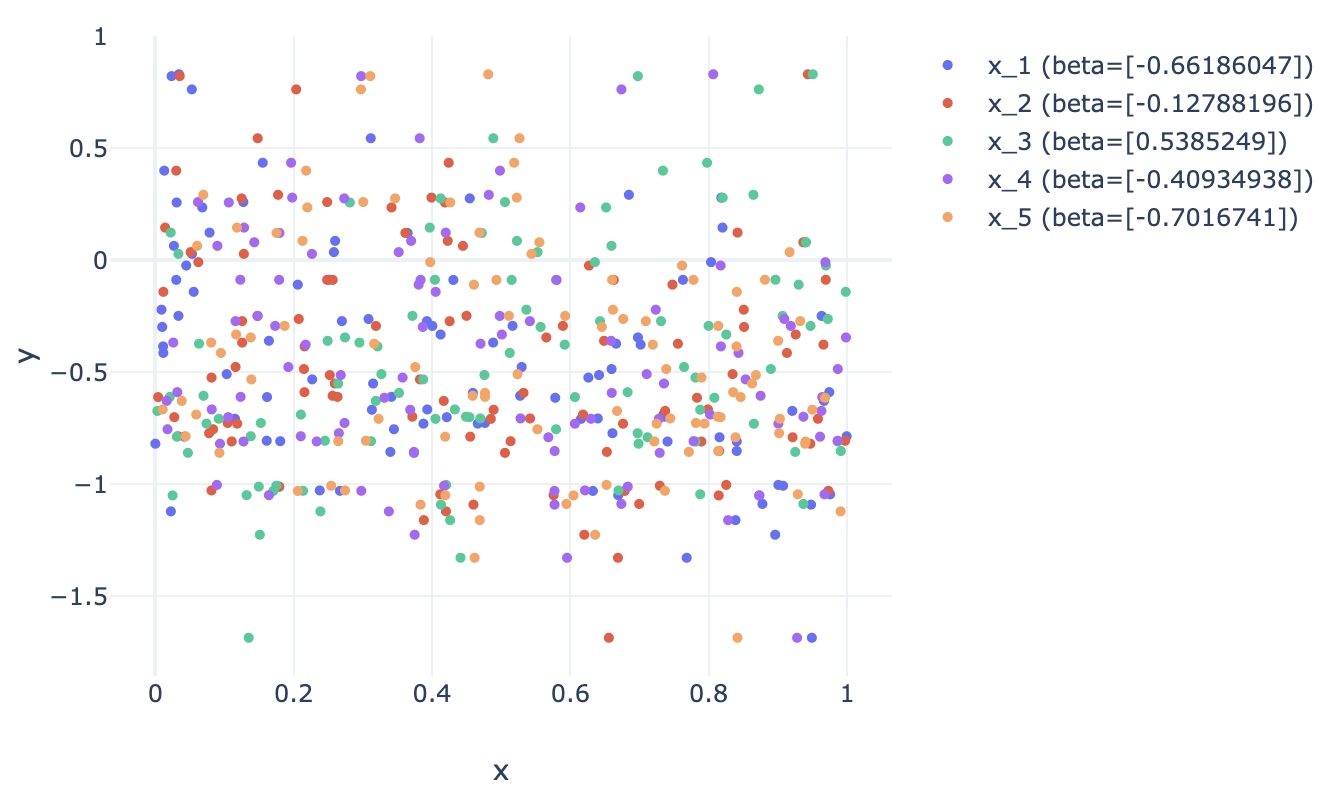
y_observed = np.matmul(X, beta_true) + e

各次元での $x_{i\cdot}$ と $y_i$ の関係は下のプロットのようになった (画像をクリックすると interactive plot が開く)。 $\beta$ が大きい次元ほどデータの相関の傾向が強い。

最尤推定

ノイズの分散 $\sigma^2$ はサンプル間で等しいとしているので、最尤推定 = 最小二乗法となる。正規方程式を解析的に解くか、もしくは尤度関数を数値最適化手法で解く。

最小二乗法 (正規方程式)

正規方程式の解 $\hat{\beta}=(X^{\top}X)^{-1}X^{\top}y$ を、np.linalg.invを信じてそのまま計算する。 $O(D^3)$ -time かかる。

beta_normal_eq = np.linalg.inv(X.T.dot(X)).dot(X.T).dot(y_observed)

分散の推定値は $\hat{\sigma}^2=\sum_{i=1}^{N}(y_i-x_i^{\top}\hat{\beta})^2/(N-(D+1))$ となる。

最小二乗法 (数値最適化)

今回は MSE が尤度関数の最大化部分を符号反転したものと等しくなる。まずは最適化用の $\beta$ をtf.Variableとして定義する。y_estimatedは目的関数の計算に必要で、tf.Variableオブジェクトに依存しているのでtf.Tensorオブジェクトとして定義する。

beta_least_sq = tf.Variable(tf.zeros([D + 1, 1]))
y_estimated = tf.matmul(X, beta_least_sq)

あとは学習率と損失関数と最適化手法を以下のように定義する。

learning_rate = 0.1
loss = tf.reduce_mean(tf.square(y_estimated - y_observed))
optimizer = tf.train.GradientDescentOptimizer(learning_rate).minimize(loss)

そうしたら Tensorflow のセッションを開始して最適化を開始する。

sess = tf.Session()
sess.run(tf.global_variables_initializer())

n_iters = 500
for i in range(n_iters):
    if i % 50 == 0:
        print(f"Step {i}: loss = {sess.run(loss)}")
    sess.run(optimizer)

最適化後の $\hat{\beta}$ はsess.run(beta_least_sq)で呼び出せる。

ベイズ推定

求めたいのは以下の事後分布である。

p(\beta,\sigma^2\vert y)=\frac{p(\beta,\sigma^2,y)}{p(y)}=\frac{p(y\vert\beta,\sigma^2)p(\beta)p(\sigma^2)}{p(y)}

線形回帰のモデルは $y_i\sim{\rm Normal}(x_i^{\top}\beta,\sigma^2)$ と書けるので、尤度関数は次のようになる。

p(y\vert\beta,\sigma^2)=\prod_i{\rm Normal}(y_i;x_i^{\top}\beta,\sigma^2)

パラメタの事前分布はここでは次のように設定する ( $\beta_0,\Sigma_0,a_0,b_0$ はハイパーパラメタ)。

\beta\sim{\rm Normal}_{D+1}(\beta_0,\Sigma_0) \\ \sigma^2\sim{\rm InvGamma}(a_0,b_0)

しかし、周辺尤度 $p(y)=\int_{\beta}\int_{\sigma^2}p(\beta,\sigma^2,y)d\beta d\sigma^2$ は解析的に解けないので、何らかの近似推論に頼ることになる。

ギブスサンプリング

Tensorflow Probability にはギブスサンプリングを楽に行う方法は無いよう (cf. GitHub Issues; Edward2 の前身の Edward にはed.Gibbsというのがあったらしい) なので、Tensorflow は使わずに書いた。

ギブスサンプリングを行うには、各パラメタの完全条件付き分布 $p(\beta\vert\sigma^2,y),p(\sigma^2\vert\beta,y)$ が必要になる。これらは自分で求めておく必要があって、それぞれ

\beta\vert\sigma^2,y\sim{\rm Normal}_{D+1}(\beta',\Sigma') \\ \sigma^2\vert\beta,y\sim{\rm InvGamma}\left(\frac{N}{2}+a_0,\frac{\sum_{i=1}^{N}(y_i-x_i^{\top}\beta)^2}{2}+b_0\right)

となることが知られている。ただし、

\Sigma'=\left(\sum_{i=1}^{N}\frac{x_ix_i^{\top}}{\sigma^2}+\Sigma_0^{-1}\right)^{-1} \\ \beta'=\Sigma'\left(\sum_{i=1}^{N}\frac{x_iy_i}{\sigma^2}+\Sigma_0^{-1}\beta_0\right)

である。これらの分布を用いて $\beta$ と $\sigma^2$ を交互にサンプリングすることで最適化を行う。

まずはハイパーパラメタの値を決める。ここでは探索せずに決め打ちする。

beta0 = np.zeros([D + 1, 1], dtype=np.float32)
sigma0 = np.identity(D + 1, dtype=np.float32)
a0 = 1.
b0 = 0.5

次に各パラメタのサンプリングを行う関数を定義する。多変量正規分布からのサンプリングにはnp.random.multivariate_normalを、逆ガンマ分布からのサンプリングにはscipy.stats.invgamma.rvsを、それぞれ使った。

# constants
sigma0_inv = np.linalg.inv(sigma0)
sigma0_beta0_dot = sigma0_inv.dot(beta0)
X_square_sum = np.sum([np.outer(X[i], X[i]) for i in range(N)], axis=0)
xy_square_sum = np.sum([X[i] * y_observed[i] for i in range(N)], axis=0)

def sample_beta(noise_var):
    """Sample beta given noise_var."""
    sigma_prime = np.linalg.inv(X_square_sum / noise_var + sigma0_inv)
    beta_prime = sigma_prime.dot(np.expand_dims(xy_square_sum / noise_var, axis=1) + sigma0_beta0_dot)
    return np.random.multivariate_normal(np.squeeze(beta_prime), sigma_prime)

def sample_noise_var(beta):
    """Sample noise_var given beta."""
    a = N / 2 + a0
    b = np.sum(np.square([y_observed[i] - X[i].dot(beta) for i in range(N)]), axis=0) / 2 + b0
    return invgamma.rvs(a, scale=b)

サプリング回数とその時点での $\beta$ もしくは $\sigma^2$ どちらか一方のパラメタの値を受け取り、上の関数に基づいて両パラメタのサンプリングを指定された回数だけ行う処理をまとめた関数も用意しておく。

def do_samplings(n_iters, beta=None, noise_var=None):
    """Iteratively sample and update beta and noise_var.
    First parameter to be sampled is determined by which of beta or noise_var is passed.
    """
    assert not (beta is None and noise_var is None), "One of beta or noise_var must be passed"
    beta_first = False if beta is not None else True

    betas = np.ndarray([n_iters, D + 1])
    noise_vars = np.ndarray([n_iters])

    for i in range(n_iters):
        if beta_first:
            beta = sample_beta(noise_var)
            noise_var = sample_noise_var(beta)
        else:
            noise_var = sample_noise_var(beta)
            beta = sample_beta(noise_var)
        betas[i] = beta
        noise_vars[i] = noise_var

    return (betas, noise_vars)

そして、burn-in 期間と本番をそれぞれ指定した数だけ回す。今回は初期値として $\beta=0$ を与えてサンプリングを始めた。

n_burnin = 1000
n_iters = 3000
beta_init = np.zeros([D + 1, 1], dtype=np.float32)   # initial value
beta_samples, noise_var_samples = do_samplings(n_burnin, beta=beta_init)
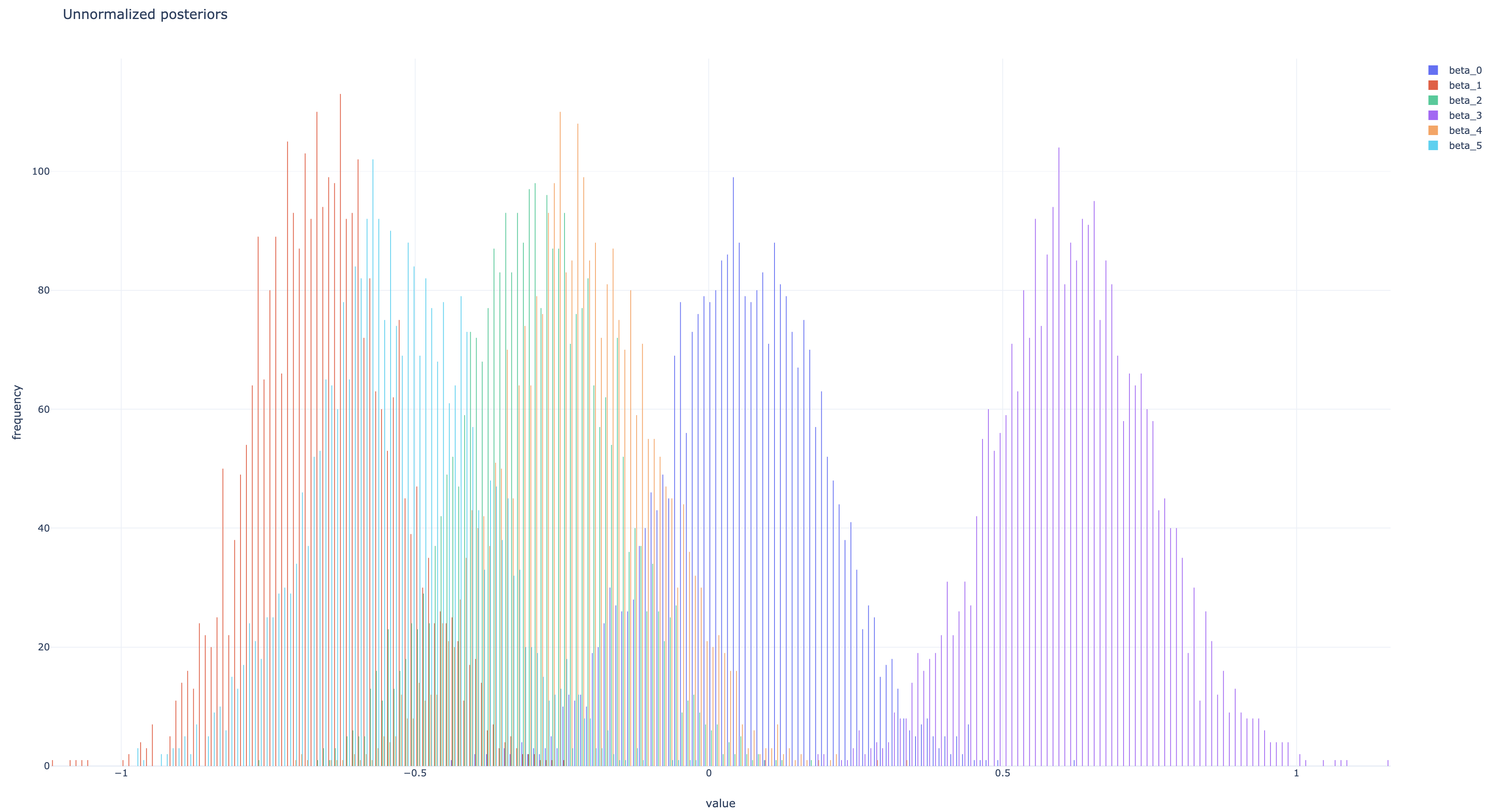
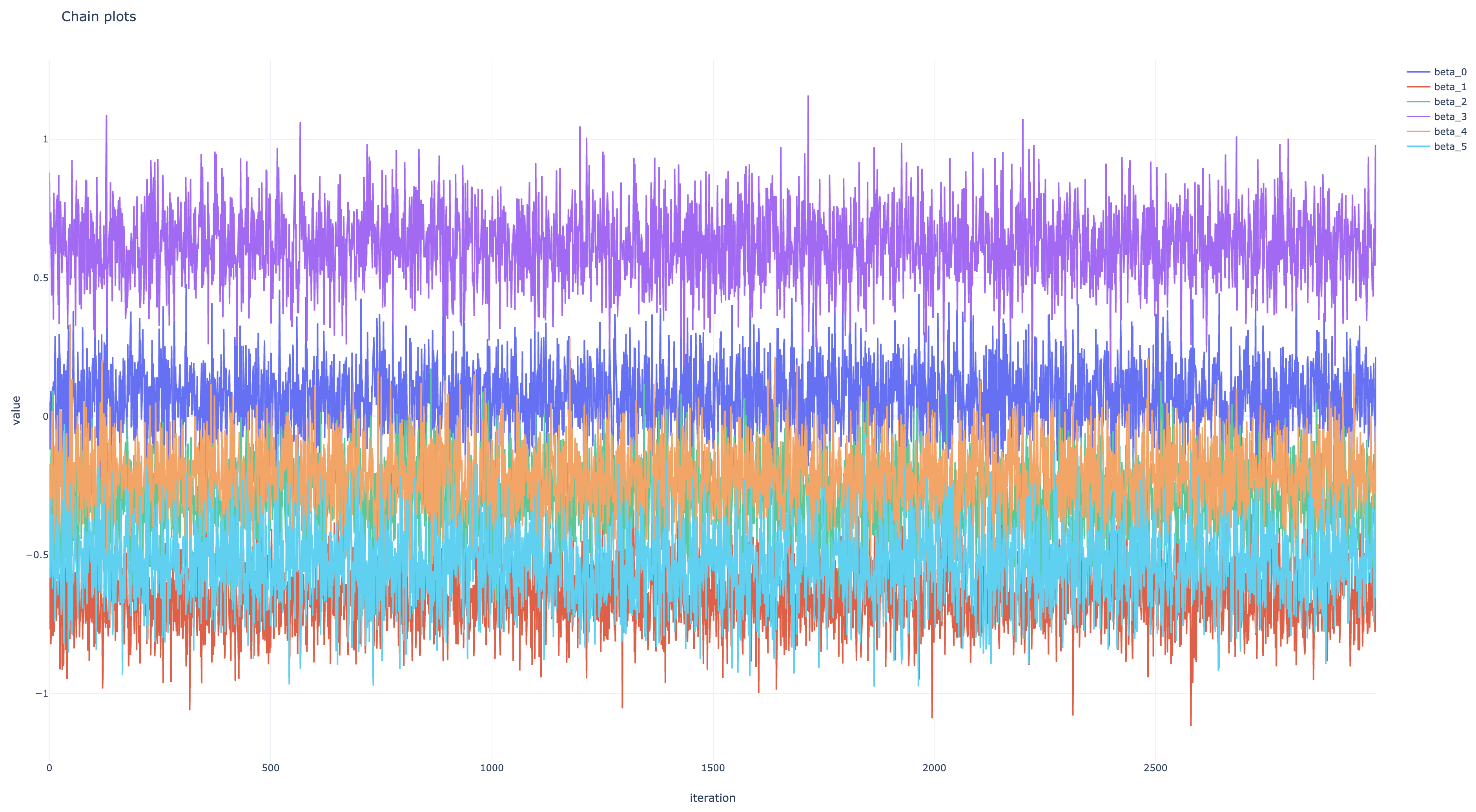
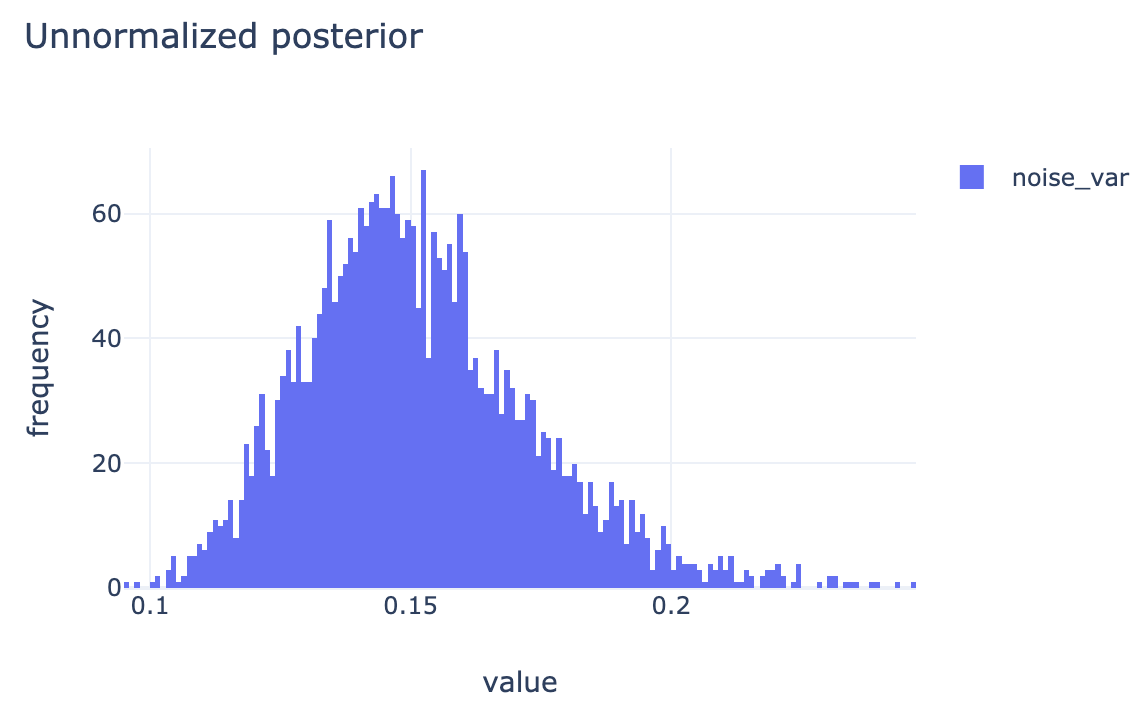
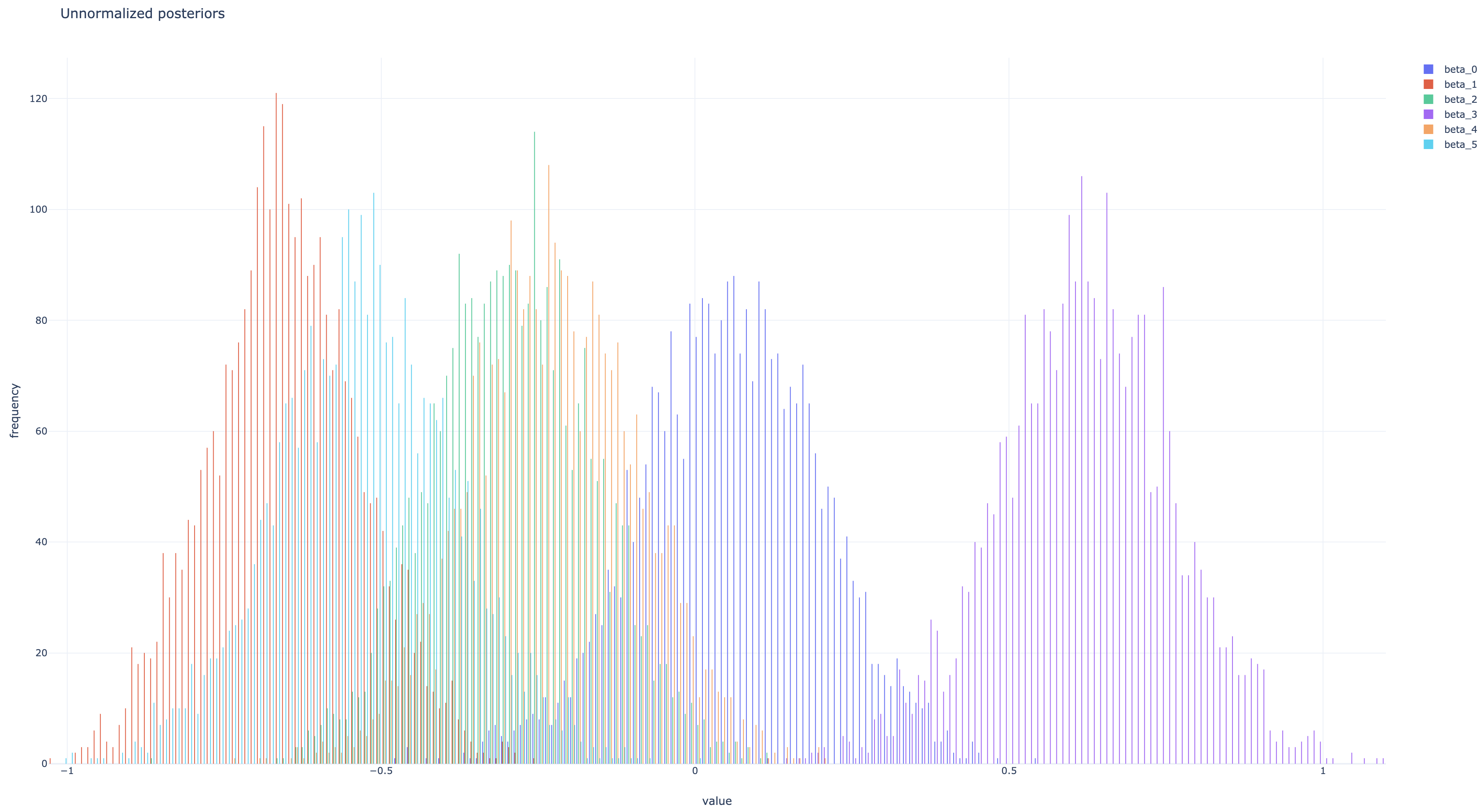
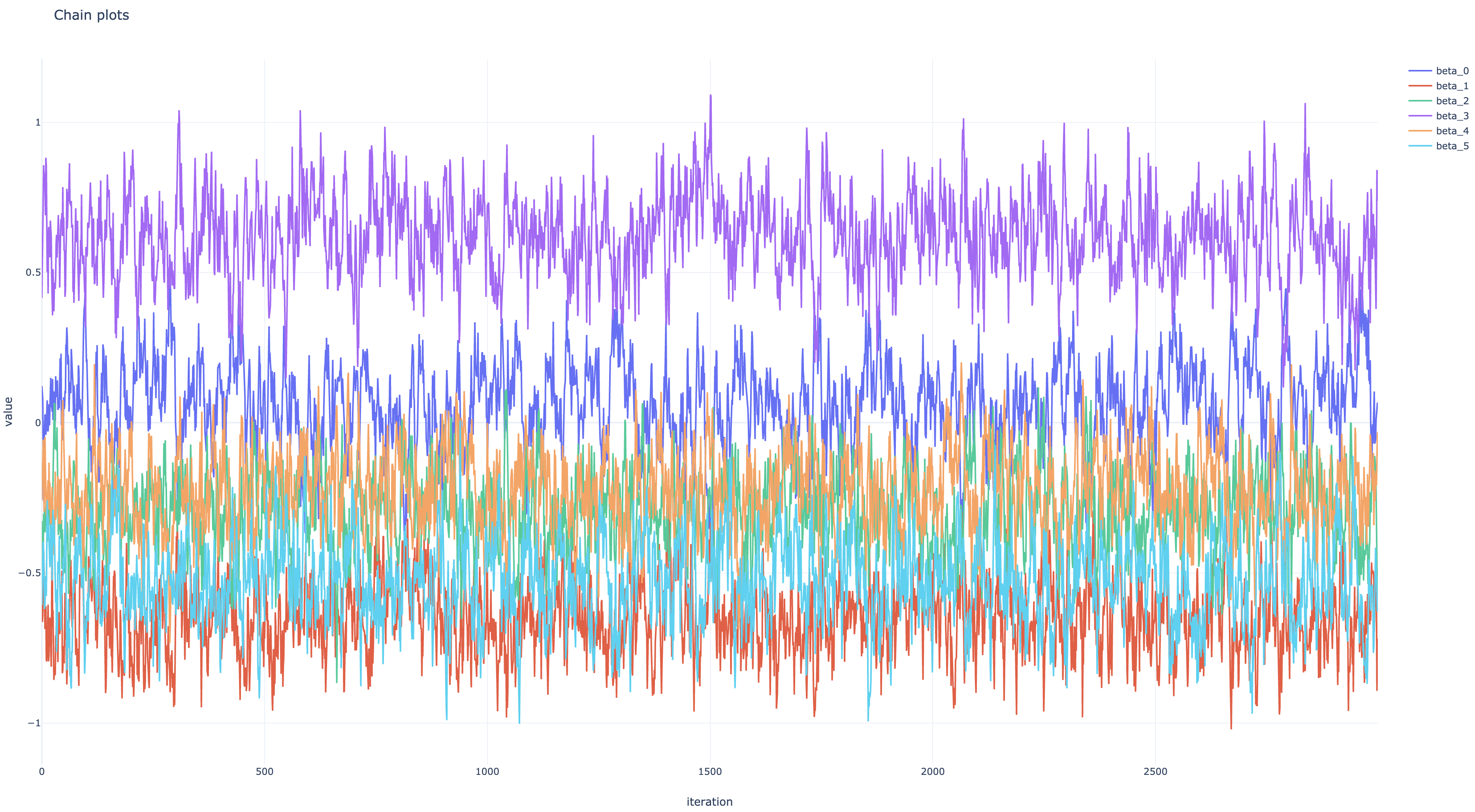
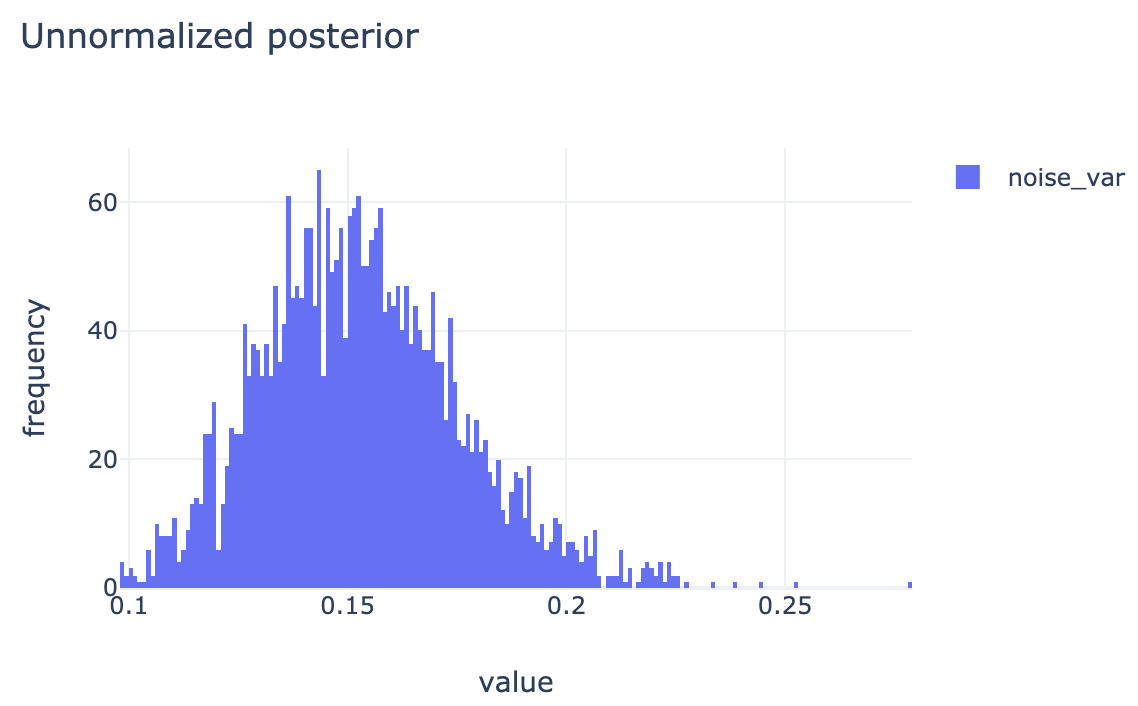
beta_samples, noise_var_samples = do_samplings(n_iters, beta=beta_samples[-1])

最終的にbeta_samples[:, i]が $\beta_i$ の、noise_var_samplesが $\sigma^2$ の、それぞれサンプル列になっているので、それらの頻度分布を正規化したものを事後分布の近似として事後平均や MAP 推定値などを求めればよい。各パラメタのサンプル列の頻度分布および推移は下の図のようになった。

ハミルトニアンモンテカルロ法

ハイパーパラメタはギブスサンプリングと同じ値を使う。

# hypterparameters
beta0 = tf.zeros([D + 1, 1], dtype=np.float32)
s0 = 1.
a0 = tf.constant(1., dtype=np.float32)
b0 = 0.5

まず、データを受け取って生成モデルのed.RandomVariableオブジェクトを返す関数を定義する。ed.Normal(...)はed.RandomVariable(tfd.Normal(...))と同じ。nameは後の計算で使うので付けておく。

def linear_regression_model(X):
    """Generative model of linear regression."""
    beta = ed.Normal(beta0, s0, name="beta")
    noise_var = ed.InverseGamma(a0, b0, name="noise_var")
    y = ed.Normal(tf.matmul(X, beta), tf.sqrt(noise_var), name="y")
    return y

次に、このモデルの関数から同時確率 $p(\beta,\sigma^2,y)$ を計算する関数を作る。これはed.make_log_joint_fn()が自動でやってくれる。

log_joint = ed.make_log_joint_fn(linear_regression_model)

そして、パラメタを受け取って同時確率 (= 正規化されていない事後確率) を返す関数を定義する。

def unnormalzed_posterior(beta, noise_var):
    return log_joint(X=X, beta=beta, noise_var=noise_var, y=y_observed)

このunnormalized_posteriorからマルコフ連鎖の推移核を作る。step_sizeはリープフロッグ法の時間刻み幅で、小さくすると採択率は高くなるが状態の推移が遅くなる。n_leapfrog_stepsは 1 回の状態提案におけるリープフロッグ法の繰り返し数で、大きくすると状態の推移は早くなるが計算時間が増える。NUTS サンプラーはこの 2 つのパラメタを自動で決める。

step_size = 0.01
n_leapfrog_steps = 10
hmc_kernel = tfp.mcmc.HamiltonianMonteCarlo(unnormalzed_posterior, step_size, n_leapfrog_steps)

そうしたら、作成した推移核に基づいて MH 法によるサンプリングを行う (処理の定義をする)。

n_burnin = 100
n_iters = 1000
beta_init = tf.zeros([D + 1, 1], dtype=np.float32)
noise_var_init = tf.constant(1., dtype=np.float32)

(betas, noise_vars), kernel_results = tfp.mcmc.sample_chain(n_iters,
                                                            [beta_init, noise_var_init],
                                                            num_burnin_steps=n_burnin,
                                                            kernel=hmc_kernel)

実際のサンプリングは Tensorflow のセッションを開始して行う。

sess = tf.Session()
beta_samples, noise_var_samples, is_accepted = sess.run([betas, noise_vars, kernel_results.is_accepted])

*_samplesはギブスサンプリングのものより 1 次元多いので、同じように扱いたい場合はnp.squeeze(*_samples)する。また、np.mean(is_accepted)は MH 法の採択率になる。各パラメタのサンプル列の頻度分布および推移は下の図のようになった。

変分推論

TODO

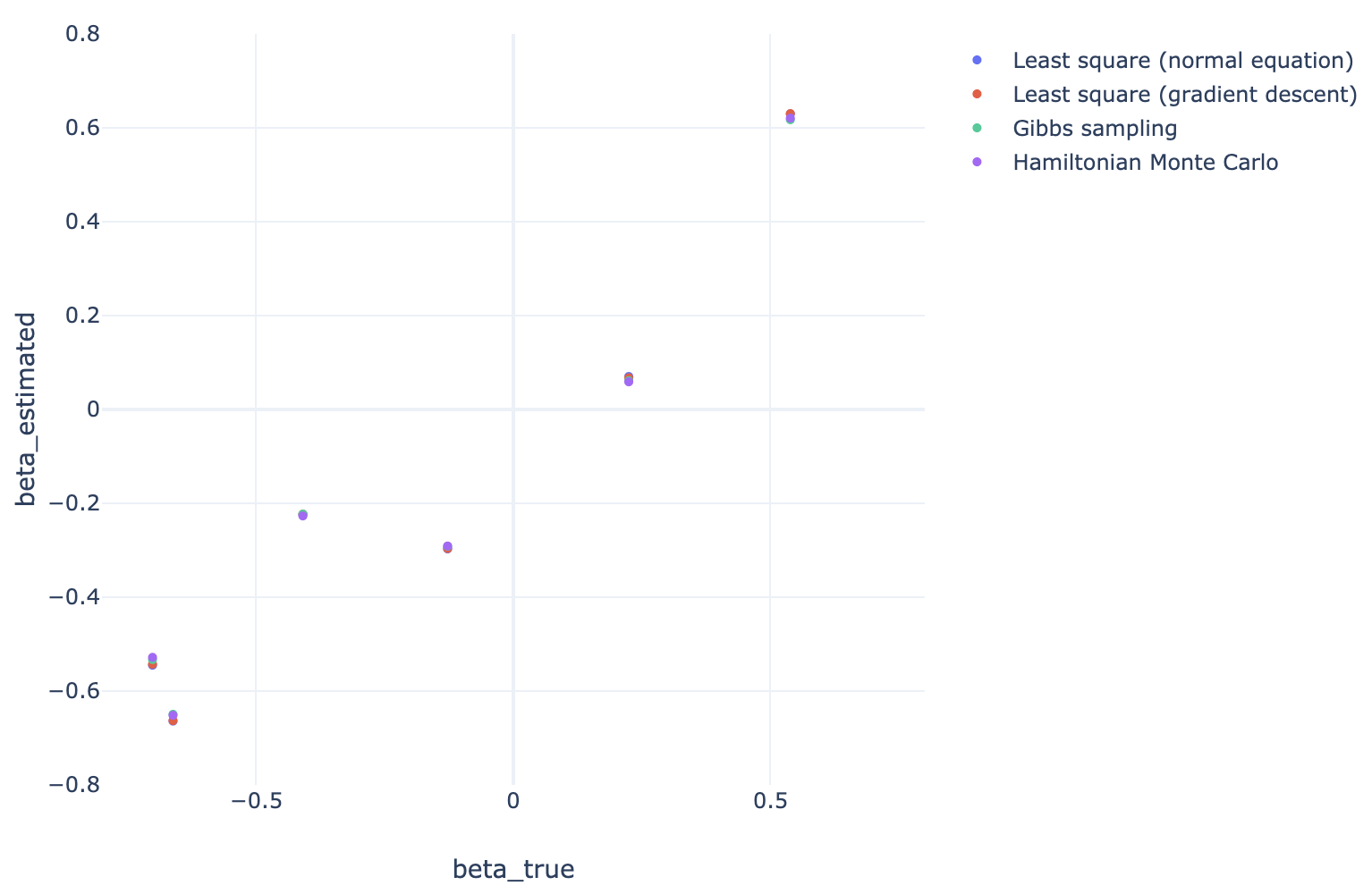
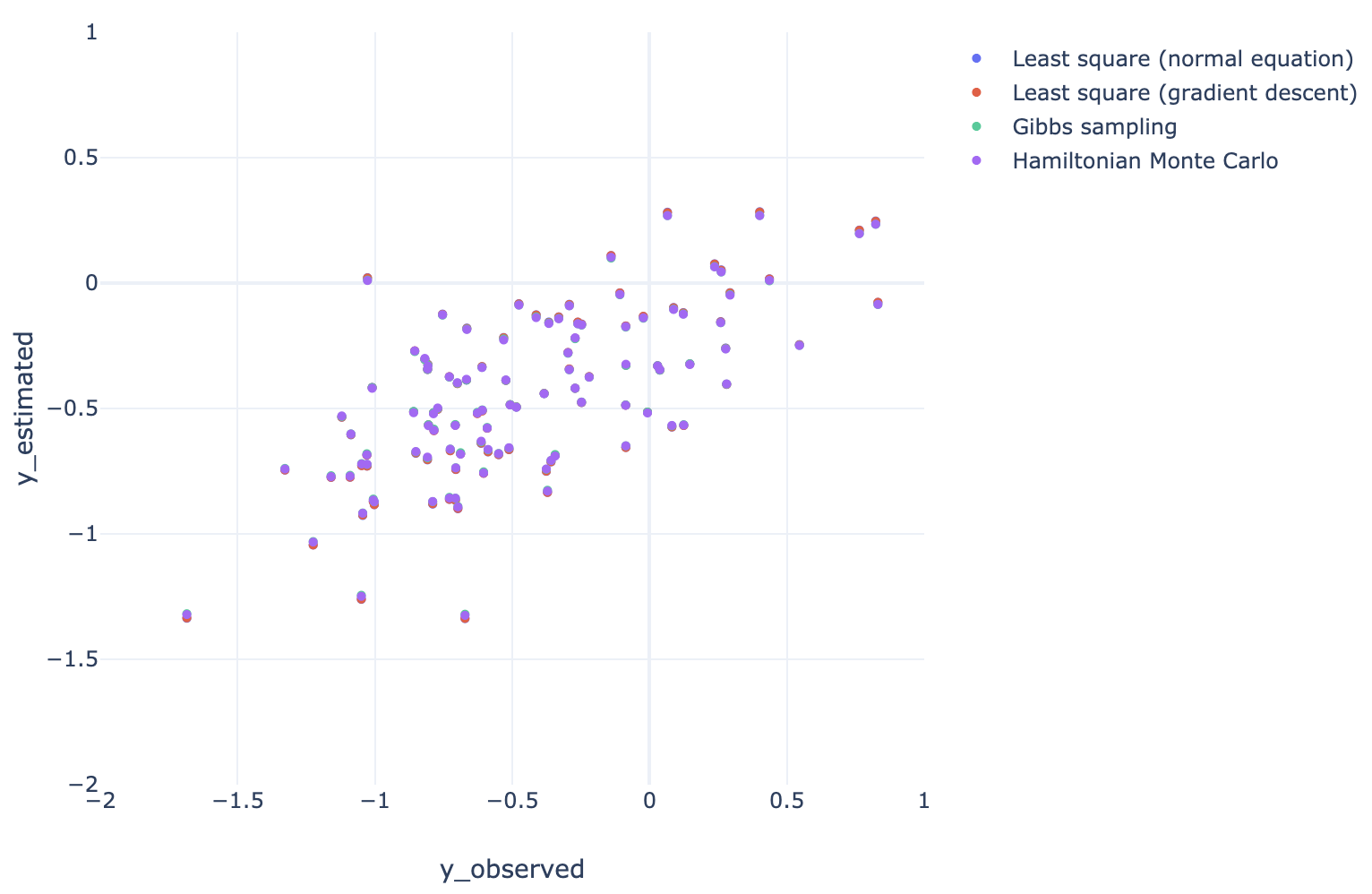
結果比較

真の $\beta,\sigma^2$ と各手法で推定された $\hat{\beta},\hat{\sigma}^2$ のプロット、および、観測された $y$ と推定された真の値 $\hat{y}=X\hat{\beta}$ のプロットは以下のようになった。すべての手法で結果がほぼ一致している。

参考文献

Published 6 Sep 2019